Chapter 19 - Making your 1st Robot - IR Line following Robot

Line/Path following Robot:

The line following robot is a mobile machine that can detect and follow a line drawn on the floor. The path is predefined and can be either visible, like a black line on a white surface, or invisible like a magnetic field emitted from a buried underground cable.

Professional line following robots is used in factories & warehouses to assist with the automated production process. Other not-so-obvious path-following robots come in various shapes, such as drones used in military applications, delivery services, or even a city-wide automated public transportation system.

I believe this would be a great start for everyone when building their very first robot. It is not a complex robot yet challenging enough to keep one engaged. Completing this robot construction task would let you experience firsthand applying the programming knowledge gained before this chapter & adequately demonstrate a simple robot controlled via a basic control system.

The Path:

Create a non-overlapping path on a large sheet of white paper using the black electrical tape found in the robotic kit.  If you do not have a large piece of paper, you can easily stick pieces of paper together with some paper tape.

 How thick should the line be?



Block diagram for the line following robot:

Here is a high-level view of the control path that our robot will be following.



The robot's task is to sense a line and maneuver accordingly to stay on course, occasionally correcting the direction it faces using a feedback mechanism, thus forming a really simple closed-loop system.


The Robot algorithm:

Try to imagine you are the robot with only the 5 channel line sensor as your sight.
(a) How many possible input scenarios would you encounter?
(b) How should you react to those input scenarios.

How do you move or steer the robot?

Our mobile robot employs a motion known as a differential drive motion control system.

The robot will move forward when the two stepper motors (& wheel) are spinning (same speed) in the opposite direction. e.g., Stepper motor on the Right spinning "Clockwise," Stepper motor on the Left spinning "Counter-Clockwise."

By us choosing a stepper motor over DC motor/servo as an actuator. If we ever set the stepper motors to spin at the same speed (in the opposite direction), our robot will travel in a straight line without much intervention. The non-linearity movement in robots using other DC motors is caused by a difference in speed as no two DC motors/servo spin at an identical speed. They will need to get a feedback mechanism either via a shaft encoder or an electronic compass to adjust the movement speed of the motors accordingly.



As you vary the speed of the Left vs. the Right stepper motor, you will notice the robot will start to swerve more strongly to the slower side.

 What will happen when you spin both Stepper motors in the same direction at the same speed? 

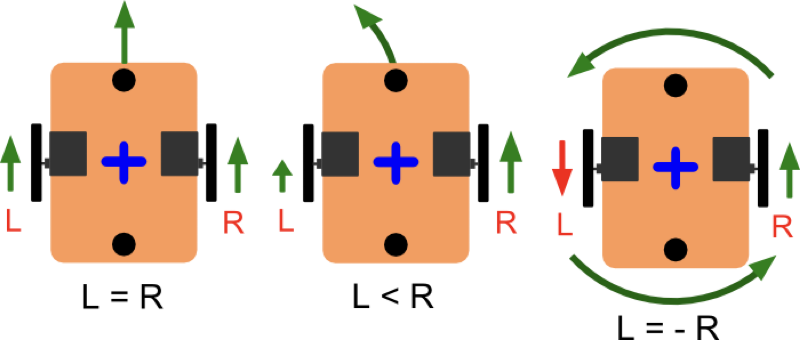
Control systems:

A control system manages or regulates the behavior of systems using control loops. 

There are two common classes of control action: open loop and closed loop.
In an open-loop control system, the control action from the controller is independent of the process variable.
An example of this is a central heating boiler controlled only by a timer. The control action is the switching on or off of the boiler. The process variable is the building temperature. This controller operates the heating system for a constant time regardless of the temperature of the building.

In a closed-loop/Feedback control system, the control action from the controller is dependent on the desired process variable.
Looking at the heating boiler example again, in this case, we would utilize a sensor/thermostat to monitor the building temperature and feedback a signal to ensure the controller maintains the building temperature close to the desired temperature set on the thermostat.



Robot Control System (PID):

Our line following robot will use a closed-loop/feedback control mechanism & will rely mainly on the 5 channel IR proximity line sensor module (Chapter 11). 
The array of 5 IR sensors on the sensor module is set up so that when the robot is perfectly centered to the black line, only the center IR sensor pair will produce a LOW signal.

Suppose the robot approached a turning/curve or simply just not centered along the path. The black line will trigger 1 or 2 sensors simultaneously at some point. Producing either a non-center signal or 2 LOW signals adjacent to each other.

The possible combination of the sensor's output when the robot is going along the path would be as follow:

The PID algorithm in the controller aims to restore the robot's direction over the black line in an optimum way, with minimal delay or overshoot, through controlling the speed output of our robot's stepper motors.

Let's have a quick recap on the Proportional Integral Derivative Control (PID control) concept. (Image from Wiki:  PID Controller)



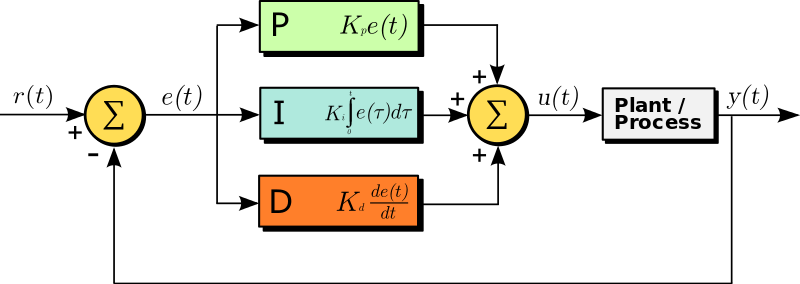
A PID controller (Line following robot controller) continuously calculates an error value e(t) as the difference between a desired setpoint r(t) and a measured process variable y(t), error value e(t)=r(t)-y(t).

Now let's add in an "Error Variable" derived from the 5 channel IR sensor reading above.
If the error variable is greater than 0, it means the path is on one side of the robot. And if the error variable is less than 0, it means the path is on the other side. Ideally, if the robot traveled along the straight line, the error variable will always remain as 0.

In the above setup (Table with the Error), The error e(t) is the difference between the current position of the robot y(t) and the desired position of the robot r(t).

Refer to the source code implementation below as: 
void readSensorValues();

Finally u(t), in the above diagram is the output from the PID controller algorithm to control the speed of the motor:
void motorControl();


Proportional Term (P):

This term is proportional to the error. It is responsible for the magnitude of change required in the physical quantity to achieve the setpoint (e(t) = 0, robot aligned properly on the line).
The error e(t) gets multiplied with Kp and forms the proportional output of the controller. 
Giving a higher Kp will increase the responsiveness of the line following robot. But if Kp is too high, it would lead to overshoots, and the robot might travel away from the path completely :)


Integral Term (I):

This term is the cumulative sum of all the previous error values. It affects the quickness of response of the system to the change from the set point.
The Integral term works to eliminate the steady-state error - the residual e(t) error after applying proportional control.
Small e(t) x Ki will cause the integral component to increase slowly. As a result, the integral output will continually increase unless the error is zero.


Differential or Derivative Term (D):

This term is the best estimate of the future trend of the error e(t) based on its current rate of change.
It works by reducing the effect of the error e(t). This slow down the rate of change of the physical quantity when it comes close to the setpoint sometimes known as the damping effect. 
Increasing the Kd parameter will cause the Line Following Robot to react more strongly to changes in the error term and increase the overall control system response speed.

Final Equation:

      PIDvalue = (Kp*P) + (Ki*I) + (Kd*D)

Source code implementation:
void calculatePID();

Where:
     Kp is the constant used to vary the magnitude of the change required to achieve the setpoint (Robot aligned properly on the line).
     Ki is the constant used to vary the rate at which the change should be brought in the physical quantity to achieve the set point.
     Kd is the constant used to vary the stability of the system. Increasing derivative term decreases overshoot and yields higher gain with stability.



Calibration:

To keep it simple, we are going to opt with Trial & Error method. In this method, the Ki and Kd terms are set to zero first and the proportional gain Kp is increased until the Line Follower Robot starts to oscillate/wobble.

 (Advance) Once you are happy with the response speed after tweaking Kp, slowly increase the value of Ki to reduce the oscillation/wobbling.
 (Advance) After Kp & Ki has been set, Increasing derivative term Kd decreases overshoot and yields higher gain with stability. The robot will return quicker to the center line.
 (Pro) Calibration might be a really painful if you need to compile & load the code every time.
Try to think along the line where you could use the Buttons (EndStop switch to increase those constant) or Serial Monitor to send the new constants down the line. 

Once we reach Module B, you will learn how you can communicate with the Robot over WIFI. " Wireless baby...."
 (Pro) Just for your own reading: Apart from Trial & Error method, another well known technique (method) used in calibration of PID control system is the Ziegler Nichols Method.
Read up more about it:  Ziegler Nichols Method Wiki
                                         Write up by MicroStar Labs


 Todo: 

• Create a path on a piece of paper (If you haven't done so)
• Implement the robot algorithm as an Arduino® sketch for the C3 CoreModule.
• Test it on your imaginary factory floor path